Energia potentzial

Txantiloi:HezkuntzaPrograma Txantiloi:Magnitude infotaula Txantiloi:Sidebar with collapsible lists Energia potentzialak bi jatorri ditu. Izan daiteke indar-eremu (grabitatorioa, elektrostatikoa, etab.) baten barruan dagoen gorputz bati lotuta dagoen energia mekanikoa, edo gorputz baten barruko indar-eremu baten existentziak sortutakoa. Energia potentzialaren unitateak energiarenak dira, eta Nazioarteko Unitate-Sisteman joule-ak (J) dira.

Energia potentziala gorputz baten gaineko indarrek egiten duten lanarekin dago lotua. Indarrak kontserbakorrak badira, hasierako puntutik bukaerako puntura mugitzeko egin den lana bi puntuekin lotutako energia potentzialen arteko aldea da.

Energia potentzialaren kontzeptua fisikako esparru askotan erabiltzen da, grabitazioan eta elektromagnetismoan adibidez.

Sarrera

Energia potentzial mota asko daude, bakoitza indar batekin lotua. Adibidez, indar elastikoek energia potentzial elastikoa sortzen dute; indar grabitazionalek, energia potentzial grabitazionala; indar nuklear bortitzek eta ahulek, energia potentzial nuklearra, eta abar.

Potentzial batetik deribagarriak diren indarrei indar kontserbakor deritz. Horiek egindako lana

$W=-\mathrm{\Delta }U$

da, non $\mathrm{\Delta }U$ energia potentzialaren aldaketa den. Zeinu negatiboak esan nahi du indar-eremu baten aurka egindako lanak energia potentziala handitzen duela, eta indar-eremuak egindakoak, aldiz, energia potentziala txikitzen duela.

Sistema fisiko batek duen energia potentzialak bere posizioaren eta konfigurazioaren arabera duen energia adierazten du; energia zinetikoak, aldiz, higidurarengatik duen energia adierazten du. Sistema kontserbakor batean bi energia horien baturak konstante dirau.

Ikuspuntu intuitiboago bat ematearren, kontsidera dezagun Lurrak sortzen duen indar grabitatorioa, eta indar horrekin lotutako eremua. Pilota bat gorantz jaurtiz gero, altuera handitzean bere abiadura motelduko da energia potentzial handiagoa izango duelako, eta energia konstante mantentzeko energia zinetikoaren balioa txikitu beharko delako. Lurrazalean dagoen objektu baten energia potentziala ondorengoa da, non m objektuaren masa, g grabitatea, eta h altuera diren.

$U=mgh$

Potentziala indar disipatiboak daudenean ere erabil daiteke, hau da, energia kontserbatzen ez den kasuetan. Baina, horretarako, dagoen energia galera kontuan hartu behar da.

Energia potentzialaren balioa hura neurtzeko erreferentzia puntuaren arabera aldatzen da; horregatik, askotan esaten da inporta duena bi konfigurazioren arteko aldakuntza dela.

Lana eta indarra

Fitxategi:Lana eta potentzia fisikakontzeptuak modu errazean.webmEnergia potentziala indarrekin lotuta dago. Aplikatutako indar batek egindako lanak ez badu ibilbidearekiko menpekotasunik (indarra kontserbakorra bada), existituko da “potentzial” deritzogun funtzio bat U(x), hasierako eta bukaerako puntuetan ebaluatua izan daitekeena bi puntuen artean egindako lana lortzeko. Funtzio hori zeinu negatibo batekin definitu ohi da, lan positiboak potentzialaren txikitzea ekar dezan,

$W=\underset{C}{\int }𝑭\cdot d𝒙=U({𝒙}_A)-U({𝒙}_B)$

non C A-tik B-rako ibilbidea den. Lana ibilbidearekiko independentea denez, edozein C-rako beteko da.

Lana definitzen duen lerro-integralak forma berezia hartzen du F indarra eremu eskalar baten (Φ(x)) gradientea bada

$𝑭=\mathrm{\nabla }\mathrm{\Phi }=(\frac{\partial \mathrm{\Phi }}{\partial x},\frac{\partial \mathrm{\Phi }}{\partial y},\frac{\partial \mathrm{\Phi }}{\partial z})$

Kasu horretan lanaren adierazpena hau da:

$W=\underset{C}{\int }𝑭\cdot d𝒙=\underset{C}{\int }\mathrm{\nabla }\mathrm{\Phi }\cdot d𝒙$

Gradientearen teorema erabilita honakoa geratzen da:

$W=\mathrm{\Phi }({𝒙}_B)-\mathrm{\Phi }({𝒙}_A)$

DipoloTxantiloi:Apurtutako esteka elektriko batek sortutako eremuaren gainazal ekipotentzialak.

Kalkuluen erraztasun horrengatik askotan saiatuko gara aplikatutako indarrarekin honela erlazionatutako potentzial eskalarra lortzen.

$𝑭(𝒓)=-\mathrm{\nabla }V(𝒓)$

Zeinu negatiboarekin definitu ohi da, indar erakarle batek potentzialaren gradiente (aldaketa espazial) positibo bat izateko.

Gainazal ekipotentzialak

Potentzial bereko puntuak elkartzen dituzten kurbei gainazal ekipotentzial deritze. Lanaren definizioa lehen emandakoa izanik, nabaria da objektu bat gainazal berdineko puntu batetik bestera eramateko egin beharreko lana nulua dela. Adibide bat ematearren, karga puntual batek osatutako sistemaren kasuan, gainazal ekipotentzialak distantzia erradial berdinera dauden puntuek osatzen dituztenak dira.

Energia potentzial grabitatorioa

ErrusiarTxantiloi:Apurtutako esteka mendietako autoek ibilbidearen zati altuenean dute energia potentzial grabitatorio maximoa. Jaitsieran, energia zinetikoan bihurtzen da, ibilbidearen puntu baxuenean maximoa (eta energia potentziala minimoa) izanda. Ondoren, igotzen hasten denean, mugimenduaren inertziaren eraginez, energia transferentzia berriro alderantzikatuko da. Marruskadura indarra arbuiatuz, sistemaren energia totala konstante mantenduko da.

Energia potentzial grabitatorioa, definizioz, gorputzek masa izateagatik eta elkarren artean distantzia batera egoteagatik duten energia da. Magnitude handiko masen artean erakarpen-indarrak sortzen dira eta indarren intentsitateak masarekin handitzen dira. Adibidez, mugimendu planetarioan aplikatuz, masa handiena duenak, eguzkiak, grabitazio-eremu bat sortzen du, masa txikiagoko planetetan eragina duena. Aldi berean, planeta bakoitzak beste grabitazio-eremu bat sortzen du, planetatik hurbil dauden masa txikiagoetan eragina duena, hau da, sateliteetan.

Grabitazio-eremuaren eraginez, $m$ masa bat beste $M$ masa baten aurrean A puntutik B puntura eramateko egindako lana honakoa da: A puntuan $m$ masak duen energia potentziala eta B puntuan duen energia potentzialaren arteko kendura da. Lana ibilbidearen independentea da, hasierako eta bukaerako puntuen menpekotasuna du bakarrik. Propietate hori erabiliz, grabitazio-indarrari eta grabitazio-eremuari eremu kontserbakorra deritzo. Hori dela eta, energia potentzial grabitatorioa $M$ eta $m$ masen arteko grabitazio-indarretik lortu daiteke.

Grabitazio-eremuaren iturri moduan $M$ masa koordenatu sistemaren jatorria kontsideratuz eta infinitua, edozein m masak energia potentziala nulua duen puntua, erreferentziatzat hartuz, $m$ masa infinitutik A puntura eramateko egin behar den lana energia potentziala da. A puntua $r$ koordenatuak definitzen du eta A puntutik koordenatuen jatorrira dagoen distantzia da.$$W=E_{pA}-E_{pB}=$$$\mathrm{\Delta }{E}_p=-\underset{\mathrm{\infty }}{\overset{A}{\int }}{F}_g\cdot dr=-\underset{\mathrm{\infty }}{\overset{A}{\int }}\frac{G\cdot M\cdot m}{r}\cdot dr=G\cdot M\cdot m{\left[\frac{1}{r}\right]}_{\mathrm{\infty }}^A=\frac{G\cdot M\cdot m}{r_A}=E_{pA}(1)$

Non, $E_p$ $m$ masaren energia potentzial grabitatorioa den, bere balioa $m$ masaren eta $M$ masaren (grabitazioa-eremua sortzen duen masaren) $r$ distantziaren menpekoa den eta joule-tan $(J)$ neurtzen den. Bestalde, $F_g=\frac{G\cdot M\cdot m}{r_A}$ grabitazio-indarra da, $m$ masaren gainekoa eta $M$ masarekiko $r$ distantzia batera dagoena. Hori, Newtonetan $(N)$ neurtzen da. Gainera, $G$ grabitazio unibertsalaren konstantea da eta bere balioa $G=6.673\times 10^{-11}\left(\frac{N\cdot m^2}{k{g}^2}\right)$ da. Azkenik, $M$ eta $m$ masak kilogramotan $(kg)$ neurtzen dira eta bien arteko distantzia, $R$, metrotan $(m)$.

$(1)$ ekuazioak $r_A$ distantziara dauden $m$ eta $M$ masen $E_{pA}$ energia potentziala adierazten du. Ekuazio hau masa puntualetako eta simetria esferikoa duten masentzako aplikatu daiteke.

Lurrazaleko energia potentziala

$m$ masa baten energia potentziala, lurrazaletik $h$ altuerara dagoenean honakoa da:$$\mathrm{\Delta }{E}_p=m\cdot g\cdot h(2)$$Adierazpen hori $(1)$ ekuazioaren kasu partikular bat da, masa lurrazaletik altuera txiki batera dagoenean aplikagarria dena. Lurrazalarekiko $h_1$eta $h_2$ altuerak kontsideratuz, eta energia potentzial diferentzia $(1)$ekuazioaren bidez kalkulatuz egiaztatu daiteke. $R_t$ Lurraren erradioa izan da ($h_1\ll R_t$, $h_2\ll R_t$ eta $h_2>h_1$).$$\mathrm{\Delta }{E}_p=E_{p2}-E_{p1}=G\cdot M\cdot m\cdot (\frac{1}{R_t+h_1}-\frac{1}{R_t+h_2})=$$$$=E_{p2}-E_{p1}=G\cdot M\cdot m\cdot \frac{(h_2-h_1)}{R_t^2+R_t\cdot (h_2+h_1)+h_2\cdot h_1}\approx G\cdot M\cdot m\cdot \frac{h_2-h_1}{R_t^2}(3)$$Kasu horretan, $R_t\cdot h_2$, $R_t\cdot h_1$ eta $h_2\cdot h_1$ balioak arbuiagarriak dira $R_t^2$ balioarekin konparatuz.

(3) ekuazioarekin jarraituz, $g=G\cdot M\cdot m\cdot \frac{1}{R_t^2}$ izendatuz,$$E_{p2}-E_{p1}=m\cdot g\cdot (h_2-h_1)$$Eta $h_1$ energia potentzialaren jatorri bezala onartuz, adibidez, itsas mailan, eta $h_2=h$ ezarriz:$$\mathrm{\Delta }{E}_p=m\cdot g\cdot h$$Aurreko garapena kontuan hartuz, $h\ll Rt$ hurbilpena egokia dela ondorioztatu dezakegu.

Ihes-abiadura

Ihes-abiadura $m$ masako gorputz batek grabitazio-erakarpenetik ateratzeko behar duen abiadura minimoa da.

Grabitazio-indarra kontserbakorra da. Energia potentziala $E_p(r)$ $m$ masa batean honakoa da:$$E_p(r)=-G\cdot \frac{m\cdot M}{r}$$Gorputz bat grabitazio-eremutik ihes egiteko, energia totala $E_t$ positiboa edo nulua izan behar du. Hau da, energia zinetikoa energia potentzialaren berdina edo handiagoa izan behar du. Beraz, mugan dagoenean ihes-abiadura izango da.$$E_t=0$$$$E_t=E_z+E_p=0\to \frac{1}{2}\cdot m\cdot v_i^2=G\cdot \frac{m\cdot M}{r}$$$$v_i=\sqrt{\frac{2\cdot G\cdot M}{r}}=\sqrt{2}gr(m/s)$$Non $r$ distantzia $m$ eta $M$ masako gorputzen artekoa den eta $M$ masako gorputzak grabitazio-eremua sortzen duen.

Lurrazalarekiko ihes-abiadura

$G=6.674\cdot 10^{-11}\frac{N\cdot m^2}{k{g}^2}$

$M_T=5.97\cdot 10^{24}kg$

$R=6.37\cdot 10^{6}m$

Datuak ordezkatuz,

$v_i=\sqrt{\frac{2\cdot G\cdot M}{R}}\approx 11.17\cdot 10^{3}m/s$

Gorputzaren abiadura ihes-abiadura baino handiagoa bada, errazago aterako da grabitazio-eremutik.

Energia potentzial elektrikoa

Energia potentzialaren aldakuntza indar kontserbakor batek egindako lana da. Bi masen erakarpen-indarra kontserbakorra da, bi kargen arteko indar elektrikoa edo Coulomben indarra, $F_{el}$, bezala. Aldarapen-indarra zeinu berdineko kargak badira, eta erakarpen-indarra aurkako zeinukoak badira. Objektuek elkar aldaratzen dutenean, zenbat eta elkarren arteko distantzia txikiagoa izan, orduan eta energia potentzial handiagoa izango dute. Bestalde, elkar erakartzen direnean, energia potentzial handiagoa izango dute elkarren arteko distantzia handiagoa denean.

Indar kontserbakor batek egindako lana funtzio baten hasierako eta bukaerako balioen arteko aldakuntza da. Energia potentziala hasierako eta bukaerako posizioen menpekoa da, eta ez ibilbidearen menpekoa. Hori dela eta, karga elektrikoek eragindako indar elektrostatikoak kontserbakorrak direnez, indar hauek egindako lana ibilbidearen independentea izango da:$$W=\underset{A}{\overset{B}{\int }}\overrightarrow{F_{el}}\cdot \overrightarrow{dl}=E_{pA}-E_{pB}$$non $E_p$ energia potentziala den, eta $E_{pA}$ eta $E_{pB}$, A eta B posizioetako energia potentzialak.

qTxantiloi:Apurtutako esteka karga mugitzeko egindako lan elektrikoan parte hartzen duten aldagaiak, Q kargak sortutako eremu elektriko baten aurrean.

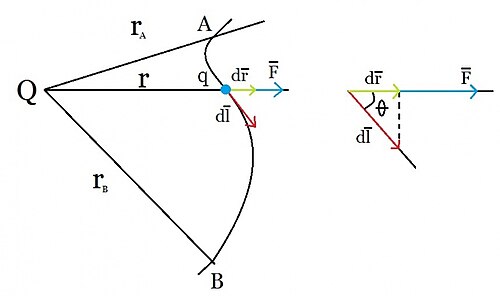
Indar elektrikoak edo elektrostatikoak, $F_{el}$, eragindako lana $W$ kalkulatzeko:$$\overrightarrow{F_{el}}=\frac{1}{4\pi {ϵ}_0}\frac{Qq}{r^2}\overrightarrow{u}=q\overrightarrow{E}$$$q$ karga A posiziotik B posiziora eramateko, lehenengo, lan infinitesimala $dW$ adierazi behar da, non $\overrightarrow{F_{el}}$ indar-bektorearen eta $\overrightarrow{dl}$ desplazamendu-bektorearen arteko biderkadura eskalarra den. $\overrightarrow{dl}$ ibilbidearen tangentea da.

Gainera, $q$ karga baten gaineko indar elektrikoa $\overrightarrow{F_{el}}=q\overrightarrow{E}$ da, non $\overrightarrow{E}$ $Q$ kargak eragindako eremu elektrikoa den. Ondorioz, oinarrizko lana $dW$ honela idatzi daiteke:$$dW=\overrightarrow{F_{el}}\cdot \overrightarrow{dl}=F_{e}dl\cos \theta =F_{e}dr=qEdr$$$dr$ $q$ kargaren desplazamendu infinitesimala izanik, $Q$ kargatik $q$ kargarako norabide erradialean. ${ϵ}_0$ hutsaren permitibitate elektrikoa da.

Honela, $Q$ eta $q$ kargen arteko indar elektrikoaren eraginez, A puntutik B puntura $q$ karga eramateko egiten den lana $W$ dela kontsideratu daiteke, non $E$ eremu elektrikoa $Q$ kargak sortutakoa den. Orduan, indar elektrikoa $Q$ kargak sortutako eremu elektrikoaren funtzioan idatziz,$$W=\underset{A}{\overset{B}{\int }}\overrightarrow{F_{el}}\cdot \overrightarrow{dl}=\underset{A}{\overset{B}{\int }}\frac{Qq}{4\pi {ϵ}_0{r}^2}dr=-{\left[\frac{Qq}{4\pi {ϵ}_{0}r}\right]}_A^B=\frac{Qq}{4\pi {ϵ}_0{r}_A}-\frac{Qq}{4\pi {ϵ}_0{r}_B}$$Indar elektrostatikoaren eraginez egindako $W$ lana ibilbidearen independentea denez, energia potentziala honela idatzi daiteke:$$E_p(r)=\frac{1}{4\pi {ϵ}_0}\frac{Qq}{r}$$Energia potentziala eragiten duen indar elektrostatikoa aldaratzailea izango da, $Q$ eta $q$ kargak zeinu berekoak badira. Beraz, energia potentziala $r$-rekin txikituz joango da. Kargak aurkako zeinukoak badira, energia potentziala negatiboa izango da eta indar elektrostatikoa erakarlea. Dualtasun hori elkarrekintza elektrikoak sortzen du eta beste motako indar edo eremuek ez duten propietatea da, adibidez, grabitazio-indarrak.

Energia potentziala eta potentzialaren funtzioak erabiltzeko, jatorri bat finkatzea beharrezkoa da. Karga puntualak kontsideratuz, energia potentzialaren zeroa infinituan ezartzen da (non energia potentziala eta potentziala ezeztatzen diren), hau da, $r=\mathrm{\infty }$ denean, $E_p=0$ izango da, energia potentzialaren funtzioa espazioko puntu guztientzako definituz.

grafikaTxantiloi:Apurtutako esteka honetan, bi kargen arteko distantzia handitzean $E_p(r)$ nola txikitzen den ikus dezakegu, $1/r$ legeari jarraituz.

Energia potentzial elektrostatikoa erabiliz potentzial elektrikoa definitzeko, $Q$ eta $q=+1C$ kargak $r$ distantzia batera daudenean energia potentziala kontsideratzen da, non $E$ eremu elektrikoa $Q$ kargak sortzen duen. Horrela, $Q$ kargak eratutako potentziala lortuko da eta energia potentziala karga positibo unitateko izango da. Hori dela eta, $Q$ kargak $r$ distantziara sortutako potentzial elektrikoa lortzeko, nahikoa da energia potentziala, $E_p(r)$, $r$ distantziara dagoen $q$ kargarekin zatitzea.$$V(r)=\frac{E_p(r)}{q}=\frac{1}{4\pi {ϵ}_0}\frac{Q}{r}$$Non $Q$ karga koordenatuen jatorrian dagoen. Potentzial elektrikoak $r$ distantziarekin energia potentzial elektrikoaren portaera bera du.

Txantiloi:Apurtutako esteka$Q$ kargak sortutako potentziala

Indar elektrostatikoa kontserbakorra denez, $q$ kargako eta $m$ masako partikula baten energia zinetikoa eta energia potentzialaren batura konstantea izango da, hau da, $E$ energia totala konstante mantenduko da, $Q$ kargak sortutako eremuaren barruan dagoen edozein $r$ posiziorako:$$E=\frac{1}{4\pi {ϵ}_0}\frac{Qq}{r}+\frac{m{v}^2}{2}=konstante$$

Energia potentzial magnetikoa

$\mu$ momentu magnetiko batek, $B$ eremu magnetiko baten eraginpean, honako energia potentziala du:$$U=-\mu \cdot B$$Eremu batean $M$ magnetizazioa hau da:$$U=-\frac{1}{2}\int M\cdot BdV$$non integrala espazio osoan egon daitekeen, edo, baliokidea dena, $M$ nulua ez den espazioan. Energia potentzial magnetikoak ez du material magnetikoen distantziaren arteko menpekotasuna soilik, eremu barruko materialen orientazio edo lerrokatzearekin ere. Adibidez, Lurraren eremu magnetikoan iparrorratzaren orratzak energia potentzial magnetiko baxuena izango du, ipar eta hego poloekin lerrokatuta dagoenean. Kanpo-indar baten eraginez orratza mugitzen bada, Lurraren eremu magnetikoak orratzaren dipolo magnetikoari bihurdura indar bat eragiten dio, orratza berriro lerrokatuz. Orratzaren energia potentzial magnetikoa handiena izango da Lurraren eremu magnetikoaren norabide berdinean dagoenean. Bi imanen energia potentziala bien arteko distantzia eta orientazioaren menpekoa izango da. Aurkako bi polo zenbat eta bananduago egon, orduan eta energia potentzial handiagoa izango dute; eta hurbilago badaude, aldiz, txikiagoa. Bestalde, polo berdinen energia potentziala handiagoa izango da hurbil daudenean, eta txikiagoa urruntzen direnean.

Energia potentzial elastikoa

Material bat elastikoa da, hasierako posizio batetik luzatu, tiratu edota deformatzean, jatorrizko lekura bere kabuz itzultzeko gai bada. Honen adibide batzuk: malgukiak, gomazko tirak eta musika instrumentuen sokak dira. Iraganean, energia mota hori materialak distantzia urrunetara botatzeko erabiltzen zituzten (arkuetan, katapultetan…).

Deformatutako material bat beste bat baino azkarrago eta zehatzago iristen bada oreka-posiziora, hura elastikoagoa dela esaten da. Esate baterako, gomazko tirak oso erraz luzatzen dira, hala ere, ez da gitarrako soka bat bezain elastikoa. Nahiz eta azken hori deformatzeko zailagoa izan, askoz doitasun handiagoarekin itzultzen da jatorrizko luzerara.

Energia mota hau aztertzerakoan, adibide ezagunena malgukia da. Malguki baten indar berreskuratzailea luzatu den distantziaren proportzionala da. Hori adierazten duen legeari Hooke-ren legea deritzo, eta oso garrantzitsua da mota hauetako sistemetarako. Bi magnitude hauen arteko erlazioa materialaren eta formaren arabera banatzen da: Solidoetan; Young-en moduluaren bitartez adierazten da materia deformatuaren eta aplikatua izan den indarraren arteko erlazioa, likido eta gasetan; presioaren eta bolumenaren arteko aldaketari konprimagarritasuna deritzo. Malguki eta kableetan, berriz, k konstante elastikoa erabiltzen da indarra eta desplazamendua erlazionatzeko.

Hooke-ren legea

Txantiloi:Sakontzeko Robert Hooke fisikari teoriko eta esperimenal bat zen. 1660an Robert Boyle-ren laguntzaile zelarik, gaur egun ezagutzen den Hooke-ren elastikotasun legea idatzi zuen.

Hooke-renTxantiloi:Apurtutako esteka legearen irudikapena marruskadurarik gabeko lurrazalean.

Oreka-posizioan dagoen malguki bat deformatu nahi bada, egin behar zaion indarra desplazamenduaren proportzionala da. Bi magnitude hauen arteko erlazioari proportzionaltasun konstantea edo konstante elastikoa deritzo, k, materialaren berezko ezaugarri bat izanik. Honela adierazten da Hooke-ren legea:$$\overrightarrow{F_{ela}}=-kx\overrightarrow{u_x}$$non $F_{ela}$ indar elastikoa, k konstante berreskuratzailea eta x oreka-posiziotik (x=0) desplazatutako distantzia den. Ekuazioko ikur negatiboaren esanahia indar elastikoaren izaeratik dator. Esan dezakegu indar mota hori berreskuratzailea dela, malgukian lotuta dagoen gorputza beti oreka-posiziora eramaten baitu.

M masako objektu bat malguki baten bidez lotzen bada eta jatorritik x distantzia batera luzatzen bada, higidura harmoniko sinple bat sorraraziko da. Edozein sistemetan bezala, mugimendu honek energia zinetiko eta potentzial bat edukiko du, eta Hooke-ren legea indar kontserbatzaile bat izanik, bertatik energia potentziala eskuratu dezakegu, indar elastikoari kontra egiten diona.$$W=E_p(x)=\underset{0}{\overset{x}{\int }}-F_{x}dx=\underset{0}{\overset{x}{\int }}-(-kx)dx=\frac{1}{2}k{x}^2$$Lan honek, M masak x posizioan duen Ep energia potentziala adierazten du. Horretarako, x=0 jatorritzat hartu da Ep=0 izateko. Masa leku batetik bestera eramateko behar den lana kalkulatzen bada, bakarrik hasierako eta bukaerako posizioen menpekoa dela frogatzen da.$$W=E_p(x_2)-E_p(x_1)=\underset{x_1}{\overset{x_2}{\int }}-kxdx=\frac{1}{2}k(x_1^2-x_2^2)$$

Energia potentziala atomoetan

Partikula txikiak aztertzerakoan, Fisika Kuantikoa erabili behar da. Fisika klasikoko legeek ez dute behar bezala funtzionatzen, eta, beraz, beste metodo batzuekin lan egin behar da. Hori gertatzen da atomoak ikertzerakoan, distantziak hain txikiak izanik ezin baitira beste edozein objektu makroskopiko bezala aztertu. Beraz, atomoa deskribatzeko, denboraren independientea den Schrödinger-en ekuazioa ebatzi behar dugu autofuntzio (atomoa deskribatzen duen funtzioa) eta autobalioak (atomoaren energia) lortzeko. Horretarako, kasu bakoitzaren Hamiltondarra jakin behar dugu, hau da, aztertu nahi dugun sistemaren energia zinetikoa eta energia potenziala. Nukleoa geldi dagoela kontsideratuz, bakarrik elektroia mugitzen ibiliko da, eta orduan energia zinetikoa soilik elektroiarena izango da. Hasieratik esan beharra dago, elektroi bakarra duten atomoetan besterik ezin dela lortu adierazpen analitiko bat, nahiz eta Hamiltondarra beti ezaguna izan.

Atomo Hidrogenoidearen energia potentziala

Atomoa aztertzerakoan, kasurik sinpleena hidrogeno atomoa edo atomo hidrogenoidearen kasua da. Azken finean, elektroi bakarra duten atomoak. Schrödinger-en ekuazioan erabili behar den Hamiltondarra oso sinplea da. Elektroi bakarra dagoenez, energia zinetikoa eta potentziala honela adierazten dira:$$\hat{H}=-\frac{\hslash }{2m}{\mathrm{\nabla }}^2+V(r)$$non m elektroiaren masa eta V(r) elektroiaren eta nukleoaren arteko energia potentziala den, Coulomb-en legetik datorrena:$$V(r)=-\frac{1}{4\pi {ϵ}_0}\frac{Z{e}^2}{r}$$non Z atomoaren protoi kopurua, r nukleotik elektroira dagoen distantzia eta e elektroiaren karga den.

Kasu honetan soluzioa guztiz ezaguna da, eta emaitza guztiak analitikoki lor ditzakegu. Schrödinger-en ekuazioa askatuz emaitza hau lortzen da:

${\psi }_{n,l,m}=R_{n,l}(r)Y_l^m(\theta ,\varphi )$

$R_{n,l}(r)=-\sqrt{{\left(\frac{2Z}{n{a}_0}\right)}^3\frac{(n-l-1)!}{2n[(n+l)!{]}^3}}{\left(\frac{2Zr}{n{a}_0}\right)}^l{e}^{-Zr/n{a}_0}{L}_{n-l-1}^{(2l+1)}\left(\frac{2Zr}{n{a}_0}\right)$

non:

• ${\psi }_{n,l,m}$ elektroiaren autofuntzioa den.
• $L_{n-\ell -1}^{(2\ell +1)}$ Laguerre-en polinomio elkartuak diren.
• $a_0$ Bohr-en erradioa den.

• $Y_l^m(\theta ,\varphi )$ harmoniko esferikoak diren.
• n,l,m atomoei lotutako zenbaki kuantikoak diren.

Eta lortzen den autobalioa, edo beste era batera esanda: Orbital atomikoaren energia.

$E_n=-\left(\frac{Z^{2}m{e}^4}{32{\pi }^2{ϵ}_0^2{\hslash }^2}\right)\frac{1}{n^2}$

non n elektroiaren energia maila den, n=1 denean oinarrizko energia izanik.

Atomo elektroianitzak

Sistema hauen arazoa elektroi gehiago agertzen direla da. Aurreko kasuan ez bezala, orain energia potentzialaren gai berri bat agertzen da. Elektroien arteko energia potentziala:$$\hat{H}=\sum _i[-\frac{\hslash }{2m}\underset{i}{\overset{2}{\mathrm{\nabla }}}-\frac{1}{4\pi {ϵ}_0}\frac{Z{e}^2}{r_i}]+\sum _{i,j}\frac{1}{4\pi {ϵ}_0}\frac{e^2}{|\overrightarrow{r_i}-\overrightarrow{r_j}|}$$non $\overrightarrow{r_{i,j}}$ nukleotik elektroi bakoitzera dagoen distantzia den. Izatez, ekarpen zailena azken horrekin dago lotuta, $r_i$ eta $r_j$ aldagaiak nahasten dituelako. Ekarpen hura ez balitz kontuan hartuko, geratuko zen Hamiltondarra banangarria izango litzateke, eta atomo hidrogenoideari dagokion autobalio eta autofuntzioak lortuko ziren. Errazagoa izan dadin, hurbilketa modura, elektroien arteko energia potentziala perturbaziotzat jotzen da, horrela, perturbazioen teoria edo metodo bariazionala erabili al da oinarrizko egoera eta autofuntzioa modu analitiko baten lortzeko.

Energia potentzial nuklearra

Energia potentzial nuklearra, nukleo atomikoetan dauden partikulen (protoien eta neutroien) arteko energia potentziala da. Distantzia oso txikiak erabiltzen direnez (fm ingurukoak $1fm=10^{-15}m$ ) Fisika Kuantikoaren arauak aplikatu behar dira. Nukleoaren barruan bi indar mota daude. Batetik, indar elektromagnetikoa; protoien kargek sortzen dutena, eta, bestetik, indar nuklearrak. Azken hauen inguruan propietate batzuk jakitea komeni da behar den energia potentzialarekin lotzeko.

• Protoien arteko indar elektrostatikoa baino 2 magnitude ordena handiagoa da.
• Berdin jokatzen du protoiekin eta neutroiekin.
• Bakarrik lehen auzoko nukleoiei eragiten die.

Ezaugarri horiekin dirudi indar nuklearrak ez direla indar kontserbakorrak, hala ere, partikulen fisikan problemak askatzeko, Energia potentzialaren adierazpen bat behar da Schrödinger-en ekuazioan sartzeko. Indar nuklearretako; eredu analitiko, enpiriko eta grafikoak eraikitzen dira kasu ezberdinetarako, eta errealitatean funtzionatzen badute erabilitako eredua baieztatu egiten da, ez dagoelako fenomenologia nuklear guztia azaltzen duen eredurik.

Energia potentzialaren langa

PartikulaTxantiloi:Apurtutako esteka ezkerretik eskumara doa eta daukan energiaren arabera potentzial-langa gainditu ahalko du. Langak nukleoak sortutako energia potentziala adierazten du.

Positiboki kargatutako partikulak nukleo atomiko baten kontra bonbardatzen badira, horiek indar elektrostatikoa jasango dute kontrako aldera, nukleoa positiboki kargatuta dagoelako. Mota horretako problemak oso konplikatuak direnez, hurbilketak erabiltzen dira. Sistema horietarako, nukleoak sortutako energia potentziala potentzial-langa bat bezala deskribatzen dugu, hau da, konstantetzat hartzen dugu. Orduan, partikulek potentzial-langa bat gainditu beharko dute barrura sartzeko.

Langa zeharkatzeko, partikulak nukleoan dagoen energia potentziala baino energia zinetiko handiagoa eduki behar du. Partikulek behar duten energia mailetara iristeko, azeleragailu batean egon behar dira. Hala ere, badago posibilitate bat partikulak langa zeharkatzeko, nahiz eta energia nahikoa ez eduki; honi tunel-efektua deritzo.

Bibliografia

• Young, Hugh D.; Freedman, Roger A. (2009). Física Universitaria de Sears-Zemansky II (Decimosegunda edición). México: Pearson. ISBN 978-607-442-304-4.

• Segrè, Emilio (1972). Núcleos y partículas. Barcelona: Reverté. ISBN 978-842-914-170-2.

• Goldstein, Herbert; Poole, Charles P.; Safko, John L. (2001). Classical Mechanics (3 edición). Addison Wesley. ISBN 0-201-65702-3.
• Kleppner, D.; Kolenkow, R.J. (1973). An Introduction to Mechanics. McGraw-Hill. ISBN 0-07-035048-5.
• Landau, L. D.; Lifshitz, E. M. (1972). Mechanics and Electrodynamics 1. Franklin Book Company, Inc. ISBN 0-08-016739-X.
• Puente, Julio; Romo, Nicolás; Pérez, Máximo (2011). Física 2 (1ª edición). Madrid: ediciones SM. ISBN 978-84-675-4660-6.

• Feynman, Richard; Leighton, Robert B; Sands, Mathew (1987). Física (Lecturas en Física) . Mecánica Cuántica (vol. 3). Addison_Wesley Iberoamericana S. A. ISBN 9688580937.
• Feynman, Richard (1999). Lectures on Physics. Perseus Publishing. ISBN 0-7382-0092-1.

• Eisberg, R; Resnick, R (1992). Física Cuántica: átomos, moléculas, sólidos, núcleos y partículas. Limusa. ISBN 9789681804190.

• Alonso, Marcelo; Finn, Edward J. (1976). Física 1. Fondo Educativo Interamericano. ISBN 9686630015.

• Serway, Raymond A.; Jewett, John W., Jr. (2003). Física: Mécánica, Oscilaciones y Ondas, Termodinámica I (3ª edición). Madrid: Thomson-Paraninfo. ISBN 84-9732-168-5 .
• French, Anthony Phillip (1974). Mecánica Newtoniana (1ª edición). Barcelona: Reverté. ISBN 8-429-14099-9 .
• Tipler, Paul Allen; Mosca, Gene (2010). Física para la ciencia y la tecnología II (6ª edición). Barcelona: Reverté. ISBN 84-291-4382-3 .
• Resnick, Robert; Halliday, David; Krane, Kenneth S. (2003). Física I I (5ª edición). Italia: Casa Editicce Ambrossiana. ISBN 88-408-1254-7 .
• Young, Hugh D.; Freedman, Roger A. (2009). Física Universitaria de Sears-Zemansky I (Decimosegunda edición). México: Pearson. ISBN 978-607-442-288-7 .
• Thornton, S. T.; Marion, J. B. (2003). Classical Dynamics of Particles and Systems (5ª edición). Thomson. ISBN 0-534-40896-6.

Kanpo estekak

• HyperPhysics. Georgia State University (ingelesez)
• Líneas equipotenciales. Georgia State University (ingelesez)
• Movimiento elíptico. University of Colorado (ingelesez)
• ¿Qué es la Energia Pontecial?. Energyavm (gazteleraz)
• Simulación de un péndulo. University of Colorado (ingelesez)
• Principio de conservación de la energía. University of Colorado (ingelesez)
• Simulación de campo eléctrico y líneas equipotenciales. University of Colorado (ingelesez)