Hutsegite-teoria

Hutsegite-teoriek zehazten dute egitura edo elementu mekaniko batek noiz eta zein magnituderen ondorioz uzten dion bere funtzioa betetzeari. Hutsegite estatikoak aztertzeko, hau da, poliki aplikatutako indarren ondorioz gertatzen direnak, hainbat teoria desberdin planteatu izan dira.

Gorputz batean kanpoko indarrek eragiten dutenean, tentsio- eta deformazio-egoera bat agertzen da gorputzeko partikuletan. Egoera hau, indarrik egon ez denekoa baino ezegonkorragoa da. Indarra kentzean gorputza hasierako egoerara itzultzen bada, gertatutako deformazioa elastikoa izan da. Indarra kendu ondoren gorputza ez bada gai hasierako egoera berreskuratzeko, deformazioa plastikoa dela esango da; izan ere, lehengo egoera zertxobait berreskuratu arren, deformazioaren zati bat era iraunkorrean geratuko baita.

Hutsegite-teorien oinarriak

Egituretan tentsio- eta deformazio-egoerak ezagututa, materialak huts egingo duen ala ez azter daiteke.

Puntu batean dagoen tentsio-egoera ardatz bakarrekoa denean, bertan gertatzen diren aldaketak aztertzeko trakzio-saiakuntzari begiratu behar zaio. Ondoren, lortutako emaitzak egoera konplexuagoetara orokortu daitezke (bi edo hiru ardatzetara). Honetarako, hutsegitea parametro baten menpe adierazten da, huts egin duen gaitasuna identifikatuz. Hauek izan daitezke parametro posibleak:

• Tentsio normal maximoa

• Luzetarako deformazio unitario maximoa
• Tentsio ebakitzaile maximoa

• Deformazio-energiaren dentsitatea

• Distortsio-energiaren dentsitatea

• Tentsio oktaedrikoa

Tentsio egoerak huts egingo du kasuan kasuko parametroak trakzio-saiakuntzan huts egindako balioa gainditzen badu. Aldiz, aukeratutako magnitudea trakzio-saiakuntzan huts egiteko aldiunean dagoena baino txikiagoa bada, tentsio-egoera onargarria da, eta ez da materialaren hutsegiterik gertatuko.

Portaera harikorra eta portaera hauskorra

Materiala harikorra denean, hutsegiterik ez gertatzeko, mugako tentsioa isurpen-tentsioaren (${\sigma }_f$) azpitik egon behar da eta hauskorra denean, haustura-tentsioaren (${\sigma }_r$) azpitik. Tentsio-egoera orokorrak aztertzeko tentsio-baliokidea (${\sigma }_{bal}$) kontzeptua erabiltzen da. Laburbilduz, hutsegiterik ez gertatzeko ondorengoa bete behar da: ${\sigma }_{bal}\le \{\begin{array}{c}{\sigma }_f\\ {\sigma }_r\end{array}$

Tentsio normal maximoaren teoriaren adierazpen grafikoa, bi ardatzeko egoera baten kasuan.

Tentsio normal maximoaren teoria (Rankine-ren teoria)

Teoria hau material hauskorrak aztertzeko erabiltzen da eta Rankine-ren irizpidea ere esaten zaio. Irizpide honen arabera, tentsio-egoera orokorra duen puntu bateko tentsio normal maximoa tentsio onargarria baino handiagoa bada, hutsegitea gertatuko da. Tentsio normalaren maximoak tentsio nagusiak dira.

Materiala harikorra bada, hutsegiterik ez egoteko honako erlazio hauek bete beharko dira:

${\sigma }_1\le {\sigma }_{ft}$                   ${\sigma }_2\le {\sigma }_{ft}$                          ${\sigma }_3\le {\sigma }_{ft}$

${\sigma }_1\le -{\sigma }_{kt}$                 ${\sigma }_2\le -{\sigma }_{kt}$                         ${\sigma }_3\le -{\sigma }_{kt}$

Materiala hauskorra bada, ${\sigma }_f$ isurpen-tentsioa beharrean, ${\sigma }_r$ haustura-tentsioa erabili behar da.

Tentsio egoera lauaren kasuan (${\sigma }_3=0$), grafikoki azter daiteke huts egingo duen ala ez, tentsio nagusiak karratu barneko eskualdean dauden edo ez aztertuz. Aldiz, 3 dimentsioko egoeran eskualdea kubo bihurtuko litzateke.

Egoera hidrostatikoaren kasuan (${\sigma }_1={\sigma }_2={\sigma }_3=\sigma$), Rankineren irizpideak dio material hauskorretan $\sigma ={\sigma }_r$ dela onar daitekeen tentsio maximoa. Alabaina, esperimentalki frogatu da tentsio hidrostatikoa balio horretara iristean ez dela haustura gertatzen, eta balio hori baino tentsio askoz altuagoak aplika daitezkeela hutsegitea gertatu baino lehen. Beraz, nahiz eta materiala hauskorra izan, jasaten duen egoera hidrostatikoa bada, irizpide hau ez da erabilgarria.

Luzetarako deformazio unitario maximoaren teoria (Saint-Venant-en teoria)

Teoria hau Saint-Venant-ek proposatu zuen, eta hutsegitea gehiegizko luzetarako deformazioaren ondorio dela jotzen da. Matematikoki adieraziz, hutsegiterik ez egoteko, honako hau bete behar da:

${\epsilon }_1\le {\epsilon }_{ft}$                                       ${\epsilon }_2\le {\epsilon }_{ft}$                                                ${\epsilon }_3\le {\epsilon }_{ft}$

${\epsilon }_1\le -{\epsilon }_{fk}$                                     ${\epsilon }_2\le -{\epsilon }_{fk}$                                              ${\epsilon }_3\le -{\epsilon }_{fk}$

Luzetarako deformazio unitario maximoaren tentsioen egoera onargarria bi ardatzeko kasuan.

non ${\epsilon }_{ft}$ eta ${\epsilon }_{kt}$ trakziozko eta konpresioko isurpen-deformazioak diren, hurrenez hurren. Materiala harikorra izan beharrean hauskorra balitz, erlazio berdinak erabiliko lirateke, baina ${\epsilon }_f$ isurpen-deformazioa ${\epsilon }_r$ haustura-deformazioarekin ordezkatuz.

Materialaren deformazioak konpresiopean eta trakziopean berdinak direla jotzen bada, eta

${\sigma }_3=0$

eginez, Hooke-ren legearen bidez ekuazio hauek lortzen dira:

${\sigma }_1-\nu {\sigma }_2\le {\sigma }_f$

${\sigma }_2-\nu {\sigma }_1\le {\sigma }_f$

${\sigma }_1-\nu {\sigma }_2\ge -{\sigma }_f$

${\sigma }_2-\nu {\sigma }_1\ge -{\sigma }_f$

Hain zuzen, adierazpen hauek grafikora ekarrita erronbo itxurako azalera lortzen da. Egoera onargarria izan dadin, tentsio nagusien balioek irudiko poligonoaren barruan egon behar dute.

Irizpide honen tentsio baliokidea kalkulatzeko hiru tentsio nagusi erabiltzen dira: ${\sigma }_{bal}=\mid {\sigma }_i-\nu ({\sigma }_j+{\sigma }_k){\mid }_{max}$

Gaur egun irizpide hau ez da ia inoiz erabiltzen, nahiz eta zenbait material hauskor eta konposaturentzat aplika daitekeen. Material harikorretan ez du ondo aurreikusten hauen isurpena, ezta egoera hidrostatikoaren hutsegitea ere.

Tentsio ebakitzaile maximoaren teoria (Tresca-ren irizpidea)

Tentsio ebakitzaile maximoaren teoriaren eremu onargarria bi ardatzeko egoeran.

Hutsegite hau material harikorrak aztertzeko erabiltzen da, beraz, isurpena agertzen deneko tentsioa izango da muga. Hasiera batean Coulomb-ek proposatu ondoren, Trescak formulatu zuen 1865. urtean. Teoria honen arabera, aztergai den egoerako tentsio ebakitzaile maximoa isurpen tentsioa baino handiagoa bada, materialak huts egingo du.

Adierazpen grafiko laua lortzeko, bi ardatzetako egoeran oinarritu behar da $({\sigma }_3=0)$ eta ondorengo ekuazio hauek betez, tentsio onargarrien eskualdea lortuko da:

${\sigma }_1-{\sigma }_2\le {\sigma }_f$                                             ${\sigma }_1-{\sigma }_2\le -{\sigma }_f$

${\sigma }_1\le {\sigma }_f$                                                      ${\sigma }_1\le -{\sigma }_f$

${\sigma }_2\le {\sigma }_f$                                                      ${\sigma }_2\le -{\sigma }_f$

Trescaren arabera, konpresio hidrostatikoan materialak ez du sekula hutsik egingo; edozein dela aplikatutako tentsioa materialak eutsi egingo du. Esperimentalki saiakuntza eginez ikus daiteke erresistentzia altua jasateko gai dela.

Deformazio-energia maximoaren teoria (Beltrami eta Haighen teoria)

Irizpide hau bolumen-unitateko deformazio-energia elastikoan oinarritzen da. Beltrami eta Haigh zientzialariek proposatu zuten (1885) eta honela diote: tentsio-egoera orokorra duen puntu bateko deformazio-energia trakzio-saiakuntzan hutsegiteko aldiunean dagoen deformazio-energia baino handiagoa bada, hutsegitea gertatuko da.

Deformazio-energia maximoaren adierazpena tentsio nagusien espazioan adierazita.

Hauxe da deformazio-energiaren dentsitatearen adierazpena tentsioen funtzioan: $U_0=\frac{1}{2E}({\sigma }_1^2+{\sigma }_2^2+{\sigma }_3^2)-\frac{\nu }{E}({\sigma }_1{\sigma }_2+{\sigma }_1{\sigma }_3+{\sigma }_2{\sigma }_3)$

Eta honako hau da trakzio-saiakuntzan, isurpena hasten den aldiunean probetako puntuek duten deformazio-energia: $U_0=\frac{{\sigma }_f^2}{2E}$

Beraz, hutsegiterik ez egoteko bete beharrekoa: $\frac{1}{2E}({\sigma }_1^2+{\sigma }_2^2+{\sigma }_3^2)-\frac{\nu }{E}({\sigma }_1{\sigma }_2+{\sigma }_1{\sigma }_3+{\sigma }_2{\sigma }_3)\le \frac{{\sigma }_f^2}{2E}$

Hortik, hau izango da irizpide honi dagokion tentsio baliokidearen balioa: ${\sigma }_{bal}=\sqrt{({\sigma }_1^2+{\sigma }_2^2+{\sigma }_3^2)-2\nu ({\sigma }_1{\sigma }_2+{\sigma }_1{\sigma }_3+{\sigma }_2{\sigma }_3)}$

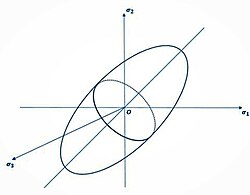
Azken adierazpena tentsio nagusien espazioan adieraziz, biraketa elipsoide bat lortzen da.

Errealitatean, ordea, irizpide hau ez da ia inoiz erabiltzen.

Distortsio-energia maximoaren teoria (Von Misesen teoria)

Von Mises-en irizpideak energia erabiltzen du oinarri gisa, baina ez guztizko deformazio-energia, honen osagai bat baizik. Irizpide hau da material harikorren isurpena zehazkien aurresaten duena. Aztergai den egoerako distortsio-energia trakzio-saiakuntzan zehaztutakoa baino handiagoa bada, materialak huts egingo du. Honetarako, tentsio-egoerak egoera hidrostatiko eta desbideratzailean deskonposatu behar dira. Beste modu batera esanda, tentsio-matrizea matrize esferikoaren (${\overrightarrow{T}}_e$) eta desbiderapen-matrizearen (${\overrightarrow{T}}_d$) batura moduan deskonposatuko da.

$\overrightarrow{T}={\overrightarrow{T}}_e+{\overrightarrow{T}}_d$

$\overrightarrow{T_e}=\left[\begin{array}{ccc}{\sigma }_b& 0& 0\\ 0& {\sigma }_b& 0\\ 0& 0& {\sigma }_b\end{array}\right]$ , $\overrightarrow{T_d}=\left[\begin{array}{ccc}{\sigma }_1-{\sigma }_b& 0& 0\\ 0& {\sigma }_2-{\sigma }_b& 0\\ 0& 0& {\sigma }_3-{\sigma }_b\end{array}\right]$

Tentsio-egoera hidrostatikoan ez dago tentsio ebakitzailerik (ez dago distortsiorik, angelu aldaketarik), soilik bolumen aldaketa gertatzen da. Aldiz, egoera desbideratzailean tentsio ebakitzaileak egongo dira, baina kasu honetan bolumen aldaketa nulua da.

Tentsio-matrizearekin egin den bezala, guztizko deformazio-energia ere bi osagairen batura modura idatz daiteke: $U_0=U_{0e}+U_{0d}$

non $U_{0e}$ eta $U_{0d}$ bolumen-aldaketari eta distortsioari dagozkien deformazio-energiak diren, hurrenez hurren. Lehenengoari dilataziozko deformazio-energia deritzo, eta bigarrenari distortsio-energia. Hain zuzen, material harikorren hutsegiteak bigarren energia mota horrekin du lotura. Dilatazio-energiak isurpenarekin zerikusirik ez duenez, ez da erabiliko.

Deformazio-energia totala:

Von Mises-en teoriaren arabera materialak hutsegiterik izango ez duen eskualdea tentsio egoera lauaren kasurako.

$U_0=\frac{1}{2E}[({\sigma }_1^2+{\sigma }_2^2+{\sigma }_3^2)-2\nu ({\sigma }_1{\sigma }_2+{\sigma }_1{\sigma }_3+{\sigma }_2{\sigma }_3)]$

Dilatazio-energia:

$U_{0e}=\frac{3{\sigma }_b^2}{2E}(1-2\nu )$ non ${\sigma }_b$ batezbesteko tentsioa den: ${\sigma }_b=\frac{{\sigma }_1+{\sigma }_2+{\sigma }_3}{3}$

Honenbestez, distortsio-energia kalkulatzeko:

$U_{0d}=U_0-U_{0e}=\frac{1+\nu }{6E}[({\sigma }_1-{\sigma }_2{)}^2+({\sigma }_1-{\sigma }_3{)}^2+({\sigma }_2-{\sigma }_3{)}^2]$

Trakzio-saiakuntzan huts egiteko momentuan ${\sigma }_1={\sigma }_f$ eta ${\sigma }_2={\sigma }_3=0$ izanik, hauxe lortzen da: $U_{0d}=\frac{1+\nu }{3E}{\sigma }_f^2$

Hortik, hutsegiterik ez egoteko, hauxe bete behar da:

$\frac{1+\nu }{6E}[({\sigma }_1-{\sigma }_2{)}^2+({\sigma }_1-{\sigma }_3{)}^2+({\sigma }_2-{\sigma }_3{)}^2]\le \frac{1+\nu }{3E}{\sigma }_f^2$

Laburki idatzita, irizpide honek isurpen-tentsioarekin parekatzen duen balioa ―tentsio baliokidea― honako hau da:

${\sigma }_{bal}=\sqrt{\frac{1}{2}[({\sigma }_1-{\sigma }_2{)}^2+({\sigma }_1-{\sigma }_3{)}^2+({\sigma }_2-{\sigma }_3{)}^2]}$

Ekuazioa bi ardatzeko egoera batentzat egokituta (${\sigma }_3=0$) elipse bat lortuko da ${\sigma }_1^2+{\sigma }_2^2+{\sigma }_1{\sigma }_2={\sigma }_f^2$ ekuazioarekin.

Emaitza berera iristen da tentsio oktaedrikoaren kontzeptuarekin eta, hau material harikorren hutsegiteak aztertzeko erabili ohi da.

Mohr-en teoria

Trakzio, konpresio eta ebakidura hutsari dagozkien Mohrren muga-zirkuluak. Zirkulu horiek guztiak inguratzen dituen kurba intrintsekoarekin.

Trakzio- eta konpresio-erresistentziak ezberdinak dituzten materialen kasuan erabiltzen da. Aztertu beharreko egoeraren irudikapena egin ostean, osagai normal jakin bati dagozkien plano posibleen artean huts egiteko arriskutsuena izango da ebakitzaile handiena duena (grafikoki Mohr-en zirkulu handienaren mugetan daudenak).

Muga hauek onargarriak diren aztertzeko saiakuntza ezberdinei dagozkien Mohrren zirkuluak definituko dira: trakzio-saiakuntzarena, konpresio-saiakuntzarena eta ebakidura-saiakuntzarena. Hiru zirkunferentzia hauek biltzen dituen kurba kurba intrintsekoa izango da.

Aztergai den tentsio-egoeraren zirkulu handiena kurba intrintsekoaren barruan badago materialak ez du huts egingo. Zirkuluaren zatiren bat kurba intrintsekotik kanpo badago, ordea, materialak huts egingo du.

Ikus, gainera

• Trakzio-saiakuntza
• Materialen erresistentzia
• Trakzio
• Elastikotasun (fisika)
• Isurpen-limite