Sinu

Sinua unitate zirkunferentzian

Matematiketan, sinua (laburtuta sin) angeluaren funtzio trigonometrikoa da. Angelu zorrotz baten sinua triangelu zuzenaren testuinguruan definitzen da: angelu espezifiko horretarako: angeluaren aurrean dagoen katetoaren luzera zati triangeluaren katetorik luzeena (hipotenusa) eginez lortzen da. $x$ angelu batentzat, sinuaren funtzioa $\sin x$ gisa adierazten da.

Orotarapena eginez, sinuaren definizioa (eta beste funtzio trigonometrikoak) edozein balio errealentzat zabaldu daiteke unitate zirkunferentziaren segmentuen luzeran neurtuta. Sinuaren definizio modernoagoek diote ekuazio diferentzialen serie infinituen soluzio bezala adieraz daitekeela, haren hedapena edozein balio positibo zein negatibo edo zenbaki konplexua izanik.

Sinuaren funtzioa fenomeno periodikoen modeloak adierazteko erabiltzen da, hala nola, soinu- eta argi-uhinak, osziladore harmonikoen posizioa eta abiadura, eguzki-argiaren intentsitatea eta egunaren luzera, eta urtean zehar gertatzen diren batez besteko tenperaturaren aldaketaren kalkulua.

Triangelu zuzenaren definizioa

Triangelu zuzen baten aldeak

α angelu zorrotzaren sinu funtzioa definitzen hasteko, α neurriko triangelu zuzen bat izan behar dugu. Alboko irudian ikus daitekeenez, guri interesatzen zaigun angelua A erpinean dagoena da. Triangeluaren hiru alboei honela deritze:

• Aurkako deritzo interesatzen zaigun angeluaren aurrean dagoen katetoari, eta kasu honentan a bezala adierazi dugu.
• Hiputenusa deritzo angelu zuzenaren aurrean dagoen aldeari, kasu honetan h. Hipotenusa triangelu zuzenaren alderik luzeena da beti.
• Albokoa da geratzen den aldea, kasu honetan b. Alde hau da aipatutako bi angeluak batzen dituena, hau da, interesatzen zaigun angelua eta angelu zuzena elkartzen dituen katetoa.

Behin triangelua definiturik, α-ren sinua aurkako aldearen luzera zati hipotenusaren luzera izango da:

$\sin \alpha =\frac{\text{aurkakoa}}{\text{hipotenusa}}$.

Unitate zirkunferentziaren definizioa

Unitate zirkunferentzian puntu beltzaren koordenatuak t angeluaren arabera

Trigonometrian, unitate zirkunferentzia bat erradiodun zirukulua da, (0, 0) puntuan (koordenatu kartesiarretan) jatorria duena.

Jatorritik hasten den lerro zuzen bat egin $x$ ardatz positiboarekin $\theta$ angelua sortzen duena, lerro zuzen hori unitate zirkunferentziarekin ebaki arte. $x$ eta $y$ koordenatuak ebakitze-puntu horretan, $\cos \theta$ eta $\sin \theta$ dira hurrenez hurren. Puntuaren jatorriarekiko distantzia beti izan da bat.

Identitateak

Animazio honetan ikus daiteke nola aldatzen doan sinu funtzioa (gorriz), angelua aldatzen den bitartean

Berdintza hauek $\theta$ angeluak har ditzakeen balio guztietarako betetzen dira,

$\sin (\theta )=\cos (\frac{\pi }{2}-\theta )=\frac{1}{\csc (\theta )}.$

Erreziprokoa

Sinuaren erreziprokoa kosekantea da, esaterako, $\sin x$ ren erreziprokoa $\csc x$ izango da. Kosekanteak hipotenusaren luzeraren ratioa aurkako aldearen luzerarekiko ematen digu.

$\csc x=\frac{1}{\sin x}=\frac{\text{hipotenusa}}{\text{aurkakoa}}=\frac{h}{a}.$

Alderantzizkoa

Sinuaren alderantzizko funtzioa arkosinua da, $\arcsin$, $\text{asin}$ edo ${\sin }^{-1}$ bezala adierazten da. Sinua funtzio injektiboa ez denez, haren alderantzizkoa ez da zehatza, alderantzizko partziala da. Adibidez, $\sin (0)=0$, baina baita $\sin (\pi )=0$, $\sin (2\pi )=0$ eta abar. Horrek esan nahi du arkusinua balio anitzeko futzioa dela: $\arcsin (0)=0$, baina baita $\arcsin (0)=\pi$, $\arcsin (0)=2\pi$, eta abar. Balio bakarra hartzen duenean, funtzioa bere adar nagusira murriztuta dagoela esan daiteke. Murrizketa horrekin, $x$ bakoitzerako $\arcsin x$ balio bakarra hartzen du eta balio nagusi deritzogu.

$\theta =\arcsin \left(\frac{\text{aurkakoa}}{\text{hipotenusa}}\right)={\sin }^{-1}\left(\frac{a}{h}\right).$

k zenbaki oso baterako,

$\begin{array}{cc}\sin (y)=x\iff & y=\arcsin x+2\pi k,\text{ edo }\\ & y=\pi -\arcsin (x)+2\pi k.\end{array}$

Ekuazio batean,

$\sin (y)=x\iff y=(-1{)}^k\arcsin (x)+\pi k.$

Arkusinuak hau betetzen du:

$\sin (\arcsin (x))=x$,

baita hau ere

$\arcsin (\sin (\theta ))=\theta \text{betez }-\frac{\pi }{2}\le \theta \le \frac{\pi }{2}.$

Kalkulua

Sinu funtziorako hau dugu:

$f(x)=\sin (x).$

Deribatua hau da:

$f^{\prime }(x)=\cos (x),$

eta, integrala berriz, hau:

$\int f(x)dx=-\cos x+C,$

non C integralaren konstantea den.

Beste funtzio trigonometriko batzuk

Posible da edozein funtzio trigonometriko beste edozein funtzio trigonometriko batzuen arabera adieraztea (plus edo minus zeinua gehituz edota sgn funtzioa erabiliz).

Sinua beste funtzio trigonometriko batzuen arabera:

	f θ	plus/minus erabiliz(±)					Sign funtzioa erabiliz (sgn)
		f θ =	± koadranteko				f θ =
			I	II	III	IV
cos	$\sin (\theta )$	$=\pm \sqrt{1-{\cos }^2(\theta )}$	+	+	−	−	$=\mathrm{sgn}(\cos (\theta -\frac{\pi }{2}))\sqrt{1-{\cos }^2(\theta )}$
	$\cos (\theta )$	$=\pm \sqrt{1-{\sin }^2(\theta )}$	+	−	−	+	$=\mathrm{sgn}(\sin (\theta +\frac{\pi }{2}))\sqrt{1-{\sin }^2(\theta )}$
cot	$\sin (\theta )$	$=\pm \frac{1}{\sqrt{1+{\cot }^2(\theta )}}$	+	+	−	−	$=\mathrm{sgn}(\cot \left(\frac{\theta }{2}\right))\frac{1}{\sqrt{1+{\cot }^2(\theta )}}$
	$\cot (\theta )$	$=\pm \frac{\sqrt{1-{\sin }^2(\theta )}}{\sin (\theta )}$	+	−	−	+	$=\mathrm{sgn}(\sin (\theta +\frac{\pi }{2}))\frac{\sqrt{1-{\sin }^2(\theta )}}{\sin (\theta )}$
tan	$\sin (\theta )$	$=\pm \frac{\tan (\theta )}{\sqrt{1+{\tan }^2(\theta )}}$	+	−	−	+	$=\mathrm{sgn}(\tan \left(\frac{2\theta +\pi }{4}\right))\frac{\tan (\theta )}{\sqrt{1+{\tan }^2(\theta )}}$
	$\tan (\theta )$	$=\pm \frac{\sin (\theta )}{\sqrt{1-{\sin }^2(\theta )}}$	+	−	−	+	$=\mathrm{sgn}(\sin (\theta +\frac{\pi }{2}))\frac{\sin (\theta )}{\sqrt{1-{\sin }^2(\theta )}}$
sec	$\sin (\theta )$	$=\pm \frac{\sqrt{{\sec }^2(\theta )-1}}{\sec (\theta )}$	+	−	+	−	$=\mathrm{sgn}(\sec \left(\frac{4\theta -\pi }{2}\right))\frac{\sqrt{{\sec }^2(\theta )-1}}{\sec (\theta )}$
	$\sec (\theta )$	$=\pm \frac{1}{\sqrt{1-{\sin }^2(\theta )}}$	+	−	−	+	$=\mathrm{sgn}(\sin (\theta +\frac{\pi }{2}))\frac{1}{\sqrt{1-{\sin }^2(\theta )}}$

Ikus bedi (±) dituzten ekuazio guztien emaitza positiboa dela angeluak lehen koadrantean daudenean.

Sinuaren eta kosinuaren arteko oinarrizko erlazioa identitate trigonometriko honen bidez adieraz daiteke:

${\sin }^2(\theta )+{\cos }^2(\theta )=1$.

Koadranteekin lotutako propietateak

Koadranteak unitate zirkunferentzian eta sinu funtzioan

Koadrantea	Graduak	Radianak	Balioa	Ikurra	Monotonia	Ganbiltasuna
1. koadrantea	$0^{\circ }<x<90^{\circ }$	$0<x<\frac{\pi }{2}$	$0<\sin (x)<1$	$+$	gorakorra	ahurra
2. koadrantea	$90^{\circ }<x<180^{\circ }$	$\frac{\pi }{2}<x<\pi$	$0<\sin (x)<1$	$+$	beherakorra	ahurra
3. koadrantea	$180^{\circ }<x<270^{\circ }$	$\pi <x<\frac{3\pi }{2}$	$-1<\sin (x)<0$	$-$	beherakorra	ganbila
4. koadrantea	$270^{\circ }<x<360^{\circ }$	$\frac{3\pi }{2}<x<2\pi$	$-1<\sin (x)<0$	$-$	gorakorra	ganbila

Serie bidezko definizioa

Aminazio honek erakusten digu Taylorren seriera zenbat eta balio gehaigo sartu, orduan eta gehiago hurbiltzen dela gure funtzioa sinuaren kurbara.

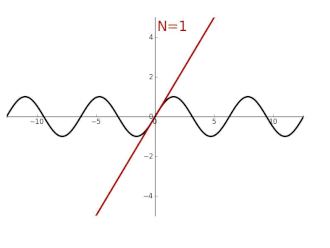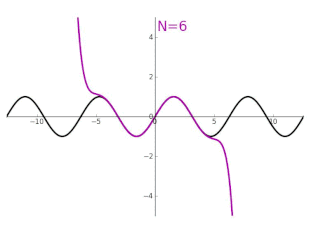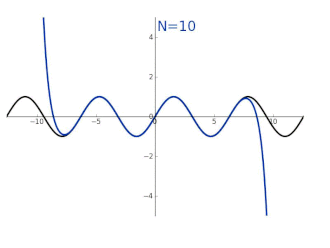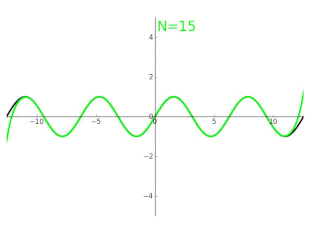
Geometria eta limiteen propietateak soilik erabiliz, ikus daiteke sinuaren deribatua kosinua dela eta kosinuaren deribatua sinuaren balio negatiboa.

Sinuaren $4n+k$-garren deribatuaren balioak 0 puntuan $k$-ren arabera emanik,

${\sin }^{(4n+k)}(0)=\{\begin{array}{ccc}0& k=0& \text{bada }\\ 1& k=1& \text{bada }\\ 0& k=2& \text{bada }\\ -1& k=3& \text{bada }\end{array}$

Horrek Taylorren seriearen hurrengo garapena ematen digu $x=0$ denean:

$\begin{array}{cc}\sin x& =x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+\cdots \\ & =\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n}{(2n+1)!}{x}^{2n+1}\\ \end{array}$

Arku-luzera

$a$ eta $b$ ren arteko sinu-kurbaren arku-luzera $\underset{a}{\overset{b}{\int }}\sqrt{1+\cos (x{)}^2}dx$ da. Integral hori bigarren motako integral eliptikoa da.

Sinuen legeak

Sinuen legeak edozein triangelurako balio du zeinak $a$, $b$ eta $c$ alboak dituzten eta albo horien aurrean dauden angeluak $A$, $B$ and $C$ izanik:

$\frac{\sin A}{a}=\frac{\sin B}{b}=\frac{\sin C}{c}.$

Goiko legea azpian ditugun lehen 3 berdintzen berdina da:

$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R,$

non $R$ triangelua zirkuskribatzen duen zirkuluaren erradioa den.

Sinuen legea triangelua bi triangelu zuzenetan banatuz eta sinuaren goiko definizioa aplikatuz frogatu daiteke. Sinuen legea erabilgarria da albo baten luzera ez dakigunean eta kalkulatu nahi dugunean, bi angeluren balioa eta albo baten luzera jakinik.

Balio bereziak

Sinuaren angelu desberdinak balio zehatzetan adierazita

Angelu batzuen balioetarako sinuen kalkulua oso erraza da, taulan ikus daitekeen bezala.

x (angelua)		sin x
Graduak	Radianak	Zehatza	Hamartarra
0°	0	0	0
180°	π
15°	Txantiloi:Sfracπ	$\frac{\sqrt{6}-\sqrt{2}}{4}$	Txantiloi:Gaps
165°	Txantiloi:Sfracπ
30°	Txantiloi:Sfracπ	Txantiloi:Sfrac	0,5
150°	Txantiloi:Sfracπ
45°	Txantiloi:Sfracπ	$\frac{\sqrt{2}}{2}$	Txantiloi:Gaps
135°	Txantiloi:Sfracπ
60°	Txantiloi:Sfracπ	$\frac{\sqrt{3}}{2}$	Txantiloi:Gaps
120°	Txantiloi:Sfracπ
75°	Txantiloi:Sfracπ	$\frac{\sqrt{6}+\sqrt{2}}{4}$	Txantiloi:Gaps
105°	Txantiloi:Sfracπ
90°	Txantiloi:Sfracπ	1	1

Zerrendan ageri ez diren bestelako balio zehatzak:

$\sin \frac{\pi }{60}=\sin 3^{\circ }=\frac{(2-\sqrt{12})\sqrt{5+\sqrt{5}}+(\sqrt{10}-\sqrt{2})(\sqrt{3}+1)}{16}$ Txantiloi:OEIS2C

$\sin \frac{\pi }{30}=\sin 6^{\circ }=\frac{\sqrt{30-\sqrt{180}}-\sqrt{5}-1}{8}$ Txantiloi:OEIS2C

$\sin \frac{\pi }{20}=\sin 9^{\circ }=\frac{\sqrt{10}+\sqrt{2}-\sqrt{20-\sqrt{80}}}{8}$ Txantiloi:OEIS2C

$\sin \frac{\pi }{15}=\sin 12^{\circ }=\frac{\sqrt{10+\sqrt{20}}+\sqrt{3}-\sqrt{15}}{8}$ Txantiloi:OEIS2C

$\sin \frac{\pi }{10}=\sin 18^{\circ }=\frac{\sqrt{5}-1}{4}=\frac{1}{2}{\phi }^{-1}$ Txantiloi:OEIS2C

$\sin \frac{7\pi }{60}=\sin 21^{\circ }=\frac{(2+\sqrt{12})\sqrt{5-\sqrt{5}}-(\sqrt{10}+\sqrt{2})(\sqrt{3}-1)}{16}$ Txantiloi:OEIS2C

$\sin \frac{\pi }{8}=\sin 22.5^{\circ }=\frac{\sqrt{2-\sqrt{2}}}{2}$

$\sin \frac{2\pi }{15}=\sin 24^{\circ }=\frac{\sqrt{3}+\sqrt{15}-\sqrt{10-\sqrt{20}}}{8}$ Txantiloi:OEIS2C

$\sin \frac{3\pi }{20}=\sin 27^{\circ }=\frac{\sqrt{20+\sqrt{80}}-\sqrt{10}+\sqrt{2}}{8}$ Txantiloi:OEIS2C

$\sin \frac{11\pi }{60}=\sin 33^{\circ }=\frac{(\sqrt{12}-2)\sqrt{5+\sqrt{5}}+(\sqrt{10}-\sqrt{2})(\sqrt{3}+1)}{16}$ Txantiloi:OEIS2C

$\sin \frac{\pi }{5}=\sin 36^{\circ }=\frac{\sqrt{10-\sqrt{20}}}{4}$ Txantiloi:OEIS2C

$\sin \frac{13\pi }{60}=\sin 39^{\circ }=\frac{(2-\sqrt{12})\sqrt{5-\sqrt{5}}+(\sqrt{10}+\sqrt{2})(\sqrt{3}+1)}{16}$ Txantiloi:OEIS2C

$\sin \frac{7\pi }{30}=\sin 42^{\circ }=\frac{\sqrt{30+\sqrt{180}}-\sqrt{5}+1}{8}$ Txantiloi:OEIS2C

Zenbaki konplexuekiko lotura

Zenbaki konplexuen planoa

Sinua koordenatu polarrentan $(r,\varphi )$ emandako zenbaki konplexuen parte irudikaria adierazteko erabiltzen da:

$z=r(\cos \phi +i\sin \phi )$,

non zati irudikaria hau den:

$\mathrm{Im}(z)=r\sin \phi$,

non $r$ eta $\varphi$ zenbaki konplexuaren luzera eta angelua diren hurrenez hurren. $i$ unitate imaginarioa da eta $z$ zenbaki konplexua.

Historia

Nahiz eta trigonometriaren azterketa Antzinaroan hasi zen, gaur egun ezagutzen ditugun funtzio trigonometrikoak Erdi Aroan garatu ziren. Soka funtzioa adibidez, Niceako Hiparkok (K.a. 180–125) aurkitu zuen.

"sin", "cos" eta "tan" laburpenak Albert Girard matematikari frantziarrak erabili zituen lehenengo aldiz XVI. mendean. Funtzio trigonometrikoak triangelu batekin definitu izan zituen lehenengoa Georg Joachim Rheticus izan zen, Kopernikoren ikaslea zena, ordura arte zirkuluen bidez definitzen baitzituzten.

1682. urtean publikatutako artikulu batean Leibnizek demostratu zuen $\sin x$ ez zela $x$-en funtzio aljebraiko bat. Bestetik, Roger Cotesek bere Harmonia Mensurarum (1722) lanean sinuaren deribatua kalkulatu zuen. Geroago, Euler bere Introductio in analysin infinitorum (1748) lanean, funtzio trigonometrikoak serie infinitu bezala definitu ahal zirela frogatu zuen eta Euler-en formula deritzon formula aurkeztu zuen.

Etimologia

Aria Bhatta (K.o. 476–550) astronomo eta matematikari hinduak sinu kontzeptuari buruzko gogoeta egin zuen, kontzeptuaz idazteko ardhá-jya izena erabiliz; ardhá "erdia" eta jya "soka" izanik. Idazle arabiarrek Bhatta-ren lan zientifikoak itzuli zituztenean, termino sanskritoa jiba izenaz adierazi zuten. Denboraren poderioz, termino hori laburtu egin zen: jb. Gerora etorri ziren idazleek, hitzaren jatorria ezagutzen ez zutenez, uste izan zuten jb jiab hitzaren laburdura zela (badia arabiarrez).

XII. mendearen amaieran, Gerardo Cremonakoa (1114–1187) itzultzaile italiarra, idazki hauek arabiarretik latinera itzultzerakoan, gaizki erabilitako jiab terminoa latinezko sinus ("zuloa", "badia") terminora itzuli zuen. Gerora, euskararen terminologia zientifikoa zehaztu zenean, latinezko terminoak oinarritzat hartu izanaren ondorioz, "sinu" denominazioa erabiltzea erabaki zen

Beste azalpen batek dio zirkulu baten soka latinez inscripta corda edo inscripta esaten denez, soka erdia semis inscriptae da. Beraz, haren laburtzapena s. ins. izango zen, gerora sins bezala sinplifikatuko zena. Hitz ezagun bati lotzearren, sinus izena jarri zitzaion.

Ikus gainera

• Kosinu
• Tangente