Azpiespazio topologia

Topologiaren arloan, X espazio topologiko baten azpiespazioa, X-ren A azpimultzo bat da X-tik heredaturiko topologia duena, azpiezpazio topologia ( edota topologia erlatiboa) deiturikoa.

Definizioa

Izan bedi $(X,{\tau }_X)$ espazio topologikoa eta $A$ $X$ -ren azpimultzoa, $A$-ren azpiezpazio topologia honela dago definituta:

${\tau }_A=\{A\cap U\mid U\in {\tau }_X\}.$

Hau da, $A$-ren azpimultzo bat irekia da azpiespazio topologikoan baldin eta solik baldin $A$-ren eta $(X,{\tau }_X)$-n irekia den multzo baten ebakidura gisa adieraz badaiteke.

${\tau }_A$azpiespazioan itxiak izango dira,${\tau }_X$espazioan itxia den eta A-ren arteko ebakidura gisa adieraz badaiteke, eta itxien multzoa $C_A$denotatuko dugu.

$A$ multzoak azpiezpazio topologia badauka, orduan, berez espazio topologikoa da, eta $(X,{\tau }_X)$-ren azpiezpazioa deritzo. Espazio topologikoen azpimultzoek azpiezpazio topologia dutela ulertzen da maiz, besterik esaten ez bada.

Propietateak

$A$, $X$-ren azpimultzo baterako azpiezpazio topologia modu honetan ere defini dezakegu: topologiarik txikiena zeinetarako partekotasun aplikazioa $ı:A\hookrightarrow X$ jarraitua den.

125x125pxTxantiloi:Apurtutako esteka

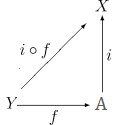
Izan bitez $A$, $X$-ren azpimultzoa eta ${ı}_A:(A,{\tau }_A)⟶(X,{\tau }_X)|{ı}_A(x)=x$ partekotasun aplikazioa.

• Orduan $(Y,{\tau }_Y)$edozein espazio topologiko baterako $f:(Y,{\tau }_Y)⟶(A,{\tau }_A)$ aplikazioa jarraitua da baldin eta soilik baldin ${ı}_A\circ f$ jarraitua bada.
• $\tau$ $A$-ren gaineko beste topologia bada non ${ı}_A:(A,{\tau }_A)⟶(X,{\tau }_X)$ jarraitua den, orduan, ${\tau }_A\subseteq \tau$.

Ondorioz, $f:(X,{\tau }_X)⟶(Y,{\tau }_Y)$jarraitua bada, orduan $f_{|A}:(A,{\tau }_A)⟶(Y,{\tau }_Y)|f(x)=x$jarraitua da. Izan ere, $f_{|A}={ı}_A\circ f$,

eta aurreko proposizioaren ondorioz, $f_{|A}$jarraitua da.

Propietate gehiago:

• $V$ ∈ ${\tau }_A$ baldin eta soilik baldin $U\in {\tau }_X$badago non $V=U\cap A$ den.
• $F\in C_A$ baldin eta soilik baldin $G\in C_X$ badago non $F=G\cap A$ den.
• $\beta$ ${\tau }_X$-ren ireki-oinarria bada, orduan, ${\beta }_A=\{B\cap A\mid B\in \beta \}$ ${\tau }_A$-ren ireki-oinarria da.
• $N\in N_x^A$ baldin eta soilik baldin $M\in N_x^X$ badago non $N=M\cap A$ den.
• $B_x$ x-ren ingurune-oinarria bada $(X,{\tau }_X)$ espazio topologikoan, orduan$B_x^A=\{B\cap A\mid B\in B_x\}$ x-ren ingurune-oinarria da $(A,{\tau }_A)$-n.
• $\sigma$ $\tau$-ren azpioinarria bada orduan ${\sigma }_A=\{S\cap A:S\in \sigma \}$${\tau }_A$-ren azpioinarria da.
• $B\subseteq A$ bada, orduan, ${\overline{B}}^A={\overline{B}}^X\cap A$ eta $B{\text{'}}^A=B{\text{'}}^X\cap A.$
• $B\subseteq A$ bada, orduan, $f{r}_A(B)\subseteq fr(B)\cap A$ eta $\stackrel{\circ }{B}\cap A\subseteq \stackrel{\circ }{B^A}$, eta berdintza ematen da $A\in \tau$ denean.

Izan bitez $(X,{\tau }_X)$ espazio topologikoa, $(A,{\tau }_A)$ eta $B\subseteq A$. $B$ $(X,{\tau }_X)$-ren azpiezpazio moduan ikus daiteke, $B$-ren gaineko ${\tau }_B$topologia erlatiboa lortuz edota $(A,{\tau }_A)$-ren azpiezpazio moduan$({\tau }_A{)}_B$topologia erlatiboa lortuz. Orduan,${\tau }_B=({\tau }_A{)}_B$

Adibideak

Hurrengoetan $ℝ$ sinboloak zenbaki errealen multzoa adierazten du ohiko topologiarekin.

• Zenbaki arrunten, $\mathbb{N}$, azpiezpazio topologia, $ℝ$-ren azpiezpazio gisa, topologia diskretua da(zenbaki osoena, $\mathbb{Z}$, ere bai) .
• Zenbaki arrazionalek, $\mathbb{Q}$, $ℝ$-ren azpiezpazio gisa,  ez dute topologia diskretua,${\tau }_{dis}$, {0} adibidez ez da multzo irekia $\mathbb{Q}$-n. a eta b arrazionalak badira, orduan (a,b) eta [a,b] tarteak irekia eta itxia dira hurrenez hurren, baina a eta b irrazionalak badira, orduan x arrazional guztien multzoa non a < x < b itxia eta irekia da.
• [0,1] multzoa $ℝ$-ren azpiezpazio gisa, itxia eta irekia da, aldiz, $ℝ$-ren azpiezpazio gisa bakarrik itxia da.
• $ℝ$-ren azpiezpazio gisa, [0, 1] ∪ [2, 3] multzoa, bi multzo ireki disjuntuek osatzen dute (itxiak ere direnak), eta, ondorioz, azpiespazio ez-konexu bat da.
• Izan bitez A = [0, 1) $ℝ$-ren azpiezpazioa . Orduan [0, 1/2) irekia da A -n, baina ez $ℝ$-n. Halaber, [½, 1) itxia da A-n, baina ez $ℝ$-n. A bai irekia eta itxia da bere buruaren azpimultzo gisa, baina ez $ℝ$-ren azpimultzo gisa.

Adibide gehiago ikasitako espazio topologikoetan

• $(X,{\tau }_{ind})$espazioan, non ${\tau }_{ind}=\{X,\mathrm{\varnothing }\}$,edozein $A\subset X$, ${\tau }_A={\tau }_{ind}$.
• $(X,{\tau }_{dis})$espazioan,non ${\tau }_{dis}=𝒫$,$X$-ren partiketa ,orduan edozein $A\subset X$, ${\tau }_A={\tau }_{dis}$
• $(X,{\tau }_{kof})$espazioan, non, ${\tau }_{kof}=\{U\subset X:X\mathrm{\setminus }U\text{ finitua da edo }U=\mathrm{\varnothing }\}$ , $A$ infinitua bada, orduan ${\tau }_A={\tau }_{kof}$ eta $A$ finitua bada, orduan ${\tau }_A={\tau }_{dis}$.
• $(X,{\tau }_{kok})$espazioan, non ${\tau }_{kok}=\{U\subseteq X:X\setminus U\text{ kontagarria da edo }A=\mathrm{\varnothing }\}$, $A$ kontagarria ez bada, orduan ${\tau }_A={\tau }_{kok}$ eta $A$ kontagarria bada, orduan ${\tau }_A={\tau }_{dis}$.

Propietate topologikoen kontserbazioa

Propietate bat heredagarria da, espazio topologiko batek propietate bat betetzeak inplikatzen badu bere edozein azpiezpaziok ere propietate hori beteko duela. Azpiezpazio itxiek soilik propietatea betetzen badute orduan ahulki heredagarri deritzo.

• Metrizagarria izatea propietate heredagarria da.
• Baire espazio baten edozein azpiezpazio ireki Baire ezpazio bat da.
• Espazio trinko baten edozein azpiespazio itxi trinkoa da.
• Hausdorff (T2) izatea propietate heredagarria da.
• Espazio normala izatea ahulki heredagarria da.

Aplikazio konbinatuak

Izan bitez X eta Y bi multzo eta $\{A_i:i\in I\}$X-ren estalkia (hau da $\underset{i\in I}{⨆}{A}_i=X$) . Demagun $f_i:A_i⟶Y$ erako aplikazioa dugula non $i\ne j$ denean $x\in A_i\cap A_j$guztietarako $f_i(x)=f_j(x)$den( $f_{i{|}_{A_i\cap A_j}}$=$f_{j{|}_{A_i\cap A_j}}$).

Orduan, $f:X⟶Y$ aplikazio konbinatua, modu honetan definituta dagoen aplikazioa da: $f:X⟶Y|f(x)=f_i(x)$ $x\in A_i$bada.

Aurreko egoeran, $(X,{\tau }_X)$eta $(Y,{\tau }_Y)$espazio topologikoak badira :

(i) $\mathrm{\forall }i\in I$, $A_i\in {\tau }_X$eta $f_i:(A_i,{\tau }_{A_i})⟶(Y,{\tau }_Y)$ jarraitua bada, orduan $f:(X,{\tau }_X)⟶(Y,{\tau }_Y)$ aplikazio konbinatua jarraitua da.

(ii) $I$ finitua bada,$\mathrm{\forall }i\in I$ , $A_i\in C_X$ eta $f_i:(A_i,{\tau }_{A_i})⟶(Y,{\tau }_Y)$ jarraituak ,orduan$f:(X,{\tau }_X)⟶(Y,{\tau }_Y)$ aplikazio konbinatua jarraitua da.

Kontradibidea

(ii) atalean, $I$ finitua izan behar da. Adibidez,$I=ℝ$bada, $1_{ℝ}:(ℝ,{\tau }_u)⟶(ℝ,{\tau }_{dis})$ ez da jarraitua, aldiz, $1_{ℝ{|}_{\{x\}}}(\{x\},{\tau }_u)⟶(ℝ,{\tau }_{dis})$ jarraitua da $x\in ℝ$guztietarako.

Murgilketak

Murgilketa bat $f:(X,{\tau }_X)⟶(Y,{\tau }_Y)$apliklikazio bat da non$f:(X,{\tau }_X)⟶(f(X),{\tau }_{f(X)})$ homeomorfismo bat den. Esango dugu $X$ $Y$-n murgilduta dagoela $f$ -ren bidez.

Murgilketa baten bidez$(X,{\tau }_X)$ espazioa $(Y,{\tau }_Y)$-ren azpiezpazio gisa ikusten da.

Propietateak

• Izan bitez $f:(X,{\tau }_X)⟶(f(X),{\tau }^{\prime })$murgilketa eta $g:(Y,{\tau }^{\prime })⟶(Z,{\tau }^{″})$ homeomorfismoa. Orduan, $g\circ f$ murgilketa da.
• Izan bedi $(X,{\tau }_X)$ espazio topologikoa eta $A$ bere azpimultzo bat ${\tau }^{\prime }$topologiarekin. Orduan, $ı:(A,{\tau }^{\prime })\hookrightarrow (X,{\tau }_X)$partekotasun aplikazioa murgilketa da baldin eta solik baldin ${\tau }^{\prime }={\tau }_A$

Ikus gainera

Zatidura espazio topologikoa

Biderkadura espazio topologikoa