Bellen zenbaki

Konbinatorian, Bellen zenbakiek multzo finituen partiketa posibleen kopurua adierazten dute. Bellen zenbakiak $B_{n}$ sinboloz adierazten dira, non $n$ zero edo handiagoa den zenbaki oso bat den. $B_{0} = B_{1} = 1$ -etik hasita.

Honako hauek dira Bellen lehenengo zenbakiak:

$1, 1, 2, 5, 15, 52, 203, 877, 4140, 21147, 115975, . . .$

Arestian definitutakoa, matematikoki ulertzeko zaila izan daitekeena, intuitiboki hobeto uler daiteke adibide bat emanez:

Pertsonen eta autoen arazoa

Pentsatu $n$ pertsona ( $n$ edozein zenbaki izanik) daudela toki batean, eta , inor kanpoan utzi gabe, autoz bidaia bat egin behar dutela. Galdera da: zenbat modutan egin dezakete bidaia hori? Galdera horrentzako erantzuna Bellen zenbakiek emango dute:

$B_{0} = 1$ : Pertsonarik ez badago, aukera bakarra dago taldekatzeko: talderik ez egitea.
$B_{1} = 1$ : Pertsona batekin, aukera bakarra dago halaber: pertsona hori auto batean sartu.
$B_{2} = 2$ : Bi pertsonarekin, bi aukera daude: bakoitza bere autoan joatea, edo biak elkarrekin joatea auto batean.
B3=5: Hiru pertsonarekin (P1,P2 eta P3); aldiz, bost aukera daude:
- Guztiak auto berean joatea.
- Bi pertsona auto berean, eta geratzen dena beste auto batean. Guztira hiru aukera dira hauek: ${P_{1}, P_{2}}$ eta ${P_{3}}$ , ${P_{1}, P_{3}}$ eta ${P_{2}}$ edo ${P_{2}, P_{3}}$ eta ${P_{1}}$ .
- Bakoitza bere autoan joatea.

Eric Temple Bell matematikariak zenbaki hauen inguruan 1930ko hamarkadan idatzi ostean haren izena jaso zuten, nahiz eta sustraiak Erdi Aroko Japonian dituzten.

Matematikoki, Bellen $n$ -garren zenbakiak, $B_{n}$ -k, $n$ elementu dituen $Ω$ multzo bat azpimultzo disjuntuetan zatitzeko modu desberdinen kopurua adierazten du, edo, baliokideki, $Ω$ multzo horren gaineko baliokidetasun-erlazio kopurua. Matematikaren arlotik kanpo, $B_{n}$ -k ematen du, adibidez, zenbat errima-eskema ezberdin dauden $n$ lerroko poementzat.

Badute beste interpretazio bat ere: probabilitate-banaketen momentu gisa. $B_{n}$ $\bar{x}$ =1 balioko Poissonen banaketaren $n$ -garren momentua da, hain zuzen ere.

Historia

Bellen zenbakiek Eric Temple Bellen omenez hartu zuten izena, Bellek idatzi baitzuen hauei buruz 1938an, Bellen polinomioak deituko zirenak aztertzen zituen 1934ko artikulu batean oinarrituta^[1]^[2].

Bellek asko lagundu zuen matematikaren garapenean. Adibidez, The Development of Mathematics liburua argitaratu zuen 1945ean, non ideia matematiko batzuen bilakaerari buruzko bertsio zabala eta interesgarria eskaintzen zuen.

Bellek ez zuen esan 1938ko bere idatzian zenbaki horiek aurkitu zituenik. 1938ko artikuluan soilik idatzi zuen zenbaki horiek "maiz ikertuak" eta "askotan berraurkituak" izan zirela. Horrez gain, zenbaki horiek matematikan duten garrantzia azpimarratu zuen.

Bellek zenbaki hauei "zenbaki esponentzialak" deitu zien; "Bellen zenbakiak" izena eta $B_{n}$ notazioa Becker eta Riordan-ek proposatu zuten 1948an^[3].

Badirudi zenbaki hauen partiketei buruzko lehen zerrenda zehatza Erdi Aroko Japonian eskaini zela, (Genjiren ipuina liburu ospetsuak inspiratuta).

Dirudienez, Erdi Aroko Japonian, Genji izeneko areto-joko bat sortu zen, non gonbidatuek bost intsentsu-pakete jasotzen zituzten usaintzeko. Gero, gonbidatuei eskatzen zitzaien asmatzeko zeintzuk ziren berdinak eta zeintzuk desberdinak euren artean.

Bost pakete horiekin, 52 irtenbide posible zeuden (gaur egun Bellen $B_{5}$ zenbakiaren bidez kalkulatu daitezkeenak). Irtenbide posible hauek 52 diagrama ezberdinen bidez erregistratu ziren eta kapituluen izenburuen gainetik inprimatu ziren Genjiren ipuina liburuaren edizio batzuetan^[4].

Bestalde, esan beharra dago XX. mende hasierako Srinivasa Ramanujan indiar matematikariak, bere bigarren koadernoan, ikertu zituela bai Bellen polinomioak bai eta Bellen zenbakiak ere^[5].

Kontaketa

Multzo baten partiketa

Orokorrean, Bellen zenbaki batek, $B_{n}$ -k, $n$ tamainako multzo baten partiketa kopurua adierazten du. $V \subseteq W$ multzoaren partiketa bat izango da baldin eta $V$ multzo hutsa ez bada; eta, gainera, $S$ -ren azpimultzo disjuntuez sortuta badago, non bere bildura $S$ bera den.

Adibideak

$B_{0} = 1$ da, zeren multzo hutsaren azpimultzo bakarra multzo hutsa bera da, hau da, $A \subseteq \emptyset ⟺ A = \emptyset$ .

$B_{3} = 5$ da, hiru elementuez osatutako multzoa, ${a, b, c}$ , bost modu ezberdinetan banatu daitekeelako. Hain zuzen ere:

${{a}, {b}, {c}}$

${{a}, {b, c}}$

${{b}, {a, c}}$

${{c}, {a, b}}$

${{a, b, c}}$

Ikus daitekeenez, aurreko multzoan erabilitako notazioari jarraituz, ez da kontuan hartu behar elementuen ordena, ezta partiketen ordena ere. Horren ondorioz, partiketa hauek guztiak berdinak dira:

${{b}, {a, c}}$

${{b}, {c, a}}$

${{a, c}, {b}}$

${{c, a}, {b}}$

Partiketen edota elementuen ordena kontuan hartuko balitz, orduan, partiketa kopurua Bellen zenbaki ordenatuek emango lukete.

Faktorizazioak

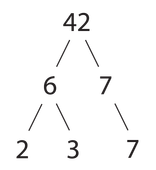
42 zenbakiaren faktorizazioa zenbaki lehenetan.

$N$ zenbaki oso bat, $n$ zenbaki lehen desberdinen biderketa gisan adieraz daitekeenean, orduan, $B_{n}$ da $N$ -ren partiketa biderkatu kopurua. Aurreko esanahiaren antzera, bi faktoriazio berdinak izango dira baldin eta beraien faktoreak berdinak badira ordena desberdin batekin.

Adibideak

$N = 30$ hartuz, $N = 2 \times 3 \times 5$ izanik; orduan, $B_{3} = 5$ da, zeren

$30 = 2 \times 15 = 3 \times 10 = 5 \times 6 = 2 \times 3 \times 5$ .

Permutazioak

Bellen zenbakiak Gardnerren gehigarria-n aipatutako karta-sortaren problema batean agertzen dira. Demagun $n$ kartako karta-sorta bat dugula. Bada, goiko karta behin eta berriz kendu eta karta-sortako edozein lekutan birtxertatuz, posizio berdinean uztearen aukera kontuan hartuz eta eragiketa hori zehatz-mehatz $n$ aldiz errepikatuz, orduan, $n^{n}$ karta-sorta egin daitezke. Horietatik, jatorrizko ordena duten sortak $B_{n}$ dira. Bestela esanda, aurreko prozesua egiteko eta karta-sorta ordenatu bat izateko probabilitatea $\frac{B_{n}}{n^{n}}$ da.

Triangeluaren bidezko eskema

Bellen zenbakiak erraz kalkula daitezke Bellen triangelua sortuz. Eskema horrek Aitkenen matrize edo Peirceren triangelu izenak ere jaso ohi ditu, Alexander Aitken eta Charles Sanders Peirceren ohorean^[6].

Triangelua honako pauso hauei jarraituz eraikitzen da:

Lehen lerroak elementu bakarra izango du: $x_{0, 1} = 1$
Lerro berri bat hasi. Lerro berri honen lehen elementua aurreko lerroko azken elementuaren berdina izango da, $x_{i, 1} = x_{i - 1, i}$
Lehen zutabean ez dauden elementuak kalkulatzeko nahikoa da ezkerretara dagoen elementua eta azken honek goian duen elementua batzearekin, $x_{i, j} = x_{i, j - 1} + x_{i - 1, j - 1}$
Hirugarren pausoa errepikatu lerro berriak aurreko lerroak baino elementu bat gehiago duen arte.
Lerro bakoitzeko lehen elementua lerro zenbaki horri dagokion Bellen zenbakia da, $x_{i, 1} = B_{i}$

Hona hemen triangeluaren lehen bost lerroak, aurreko pausoei jarraituz eraikita:

$x_{0, 1} = 1$

$x_{1, 1} = 1$ $x_{1, 2} = 2$

$x_{2, 1} = 2$ $x_{2, 2} = 3$ $x_{2, 3} = 5$

$x_{3, 1} = 5$ $x_{3, 2} = 7$ $x_{3, 3} = 10$ $x_{3, 4} = 15$

$x_{4, 1} = 15$ $x_{4, 2} = 20$ $x_{4, 3} = 27$ $x_{4, 4} = 37$ $x_{4, 5} = 52$

Ikus daitekeen bezala, $x_{0, 1} = B_{0}$ , $x_{1, 2} = B_{1}$ , $x_{2, 3} = B_{2}$ , $x_{3, 4} = B_{3}$ eta $x_{4, 5} = B_{4}$ betetzen da.

Propietateak

Batukari formulak

Bellen zenbakiek koefiziente binomialak^[7] dituen errekurtsibitate formula bat betetzen dute:

$B_{n + 1} = \sum_{k = 0}^{n} (\binom{n}{k}) B_{k}, \forall n \in ℕ \cup {0} .$

Errekurtsibitate erlazio hori hurrengo moduan azaldu daiteke: demagun $n + 1$ elementu dituen $Ω$ multzo baten partiketa bat dugula. Baldin eta partiketa horretatik lehen elementua duen multzoa kentzen bada, $k$ elementu dituen partiketa txikiago bat lortzen da, $0 \leq k \leq n$ izanik. Horrela, $(\binom{n}{k})$ aukera ditugu geratzen diren lehenengo $k$ elementuetarako, eta, definizioz, $B_{k}$ aukera.

Bellen $n$ -garren zenbakia bigarren motako Stirling zenbakien baturarekin erlazionatzen da:

$B_{n} = \sum_{k = 0}^{n} {\binom{n}{k}}, \forall n \in ℕ .$

Bigarren motako Stirling zenbakiak ${\binom{n}{k}}$ : $n$ kardinaleko multzo baten partiketa kopurua adierazten du, zehazki $k$ azpimultzo ez-hutsen existentzia bermatuz. Hortaz, aurreko berdintzan, ezkerreko partiketa bakoitza eskuineko gai batean (eta bakar batean) zenbatzen da.^[8]

2008an, Michael Z. Spiveyk aurreko bi identitateak konbinatzen dituen formula bat eman zuen:

$B_{n + m} = \sum_{k = 0}^{n} \sum_{j = 0}^{m} {\binom{m}{j}} (\binom{n}{k}) j^{n - k} B_{k} .$

Transformatu binomiala ${B_{n}}_{n \in ℕ}$ segidari aplikatuz,

$B_{n} = \sum_{k = 0}^{n} (\binom{n}{k}) (- 1)^{n - k} B_{k + 1},$

eta azken hori hurrengo moduan orokor daiteke:^[9]

$\sum_{j = 0}^{n} (\binom{n}{k}) B_{j + k} = \sum_{i = 0}^{k} (\binom{k}{i}) (- 1)^{k - i} B_{n + i + 1} .$

Lehen motako Stirling zenbakiak Bellen zenbakiak erlazionatzen dituen formula bat hurrengoa da:^[9]

$\sum_{j = 0}^{n} (\binom{n}{j}) a^{j} b^{n - j} B_{j} = \sum_{i = 0}^{k} [\binom{k}{i}] (- 1)^{k - i} \sum_{j = 0}^{n} (\binom{n}{j}) a^{j} (b - a k)^{n - j} B_{j + i} .$

$k = 1$ hartuz, hurrengo moduan sinplifikatzen da aurreko formula:

$\sum_{j = 0}^{n} (\binom{n}{j}) a^{j} b^{n - j} B_{j} = \sum_{j = 0}^{n} (\binom{n}{j}) a^{j} (b - a)^{n - j} B_{j + 1} .$

Aldiz, $a = 1$ eta $b = k$ hartuz,

$\sum_{j = 0}^{n} (\binom{n}{j}) B_{j} k^{n - j} = \sum_{i = 0}^{k} [\binom{k}{i}] B_{n + i} (- 1)^{k - i} .$

Azken hori ondoko moduan uler daiteke: trasformatu binomiala lehen motako Stirlingen zenbakiek osatutako segidari aplikatu balitzaio bezala.

Funtzio sortzailea

Bellen zenbakien funtzio sortzaile esponentziala

$B (x) = \sum_{n = 0}^{\infty} \frac{B_{n}}{n!} x^{n} = e^{e^{x} - 1}$

da. Aurreko berdintzan, batugaia zenbakien segida orokor baten funtzio sortzailea lortzeko formula da. Aldiz, berdintzaren eskuinaldeko gaina Bellen zenbakien funtzio sortzailea kalkulatzerakoan lortzen den adierazpen esplizitua da.

Bellen zenbakien funtzio sortzaile esponentziala lortzeko era alternatibo bat dago. Bellen zenbakien errekurtsibitate formulatik abiatuta, froga daiteke funtzio sortzaile esponentzialak

$B^{'} (x) = e^{x} B (x)$

ekuazio diferentziala betetzen duela. Beraz, ekuazio hori ebatziz, funtzioaren adierazpena lor daiteke.^[10]^[11]^[12]

Probabilitate banaketa

Bellen zenbakiek probabilitate gaiarekin lotura dute, bereziki, Poissonen banaketarekin. Izan ere, Bellen zenbakiek Dobińskiren formula^[13]^[14]^[15] betetzen dute, hau da,

$B_{n} = \frac{1}{e} \sum_{k = 0}^{\infty} \frac{k^{n}}{k!}, \forall n \in ℕ .$

Formula hau funtzio sortzailea garatuz lor daiteke, hain zuzen ere, funtzio esponentzialaren Taylorren seriea garatuz eta koefizienteak berdinduz^[16]. Horrela, Bellen $n$ -garren zenbakia itxarotako balioa 1eko Poissonen banaketaren $n$ -garren momentu gisa interpreta daiteke.

Aritmetika modularra

Bellen zenbakiek Toucharden kongruentzia betetzen dute: $p$ zenbaki lehena bada, orduan^[17]

$B_{p + n} \equiv B_{n} + B_{n + 1} mod p$

edo, orokortuago^[18]

$B_{p^{m} + n} \equiv m B_{n} + B_{n + 1} mod p .$

Kongruentzia hori dela eta, Bellen zenbakiak periodikoak dira modulu $p$ .

Bellen zenbaki lehenak

1978an, Martin Gardner zientzialariak Bellen zenbaki eta aldi berean zenbaki lehenak diren kopurua infinitua den ala ez planteatu zuen. Mota horretako zenbakiak Bellen zenbaki lehenak direla esaten da. Lehenengo seiak hurrengoak dira:

2, 5, 877, 27644437, 35742549198872617291353508656626642567, 359334085968622831041960188598043661065388726959079837,

Bellen $B_{2}$ , $B_{3}$ , $B_{7}$ , $B_{13}$ , $B_{42}$ eta $B_{55}$ zenbakiak izanik, hurrenez hurren. Bellen hurrengo zenbaki lehena (eta ezagutzen den Bellen zenbaki lehenik handiena) $B_{2841}$ da, gutxi gorabehera $9, 30740105 \times 1 0^{6538}$ .

Ikus, gainera

Erreferentziak

Txantiloi:Erreferentzia zerrenda

Kanpo estekak

Txantiloi:Autoritate kontrola

[1] Txantiloi:Erreferentzia

[2] Txantiloi:Erreferentzia

[3] Txantiloi:Erreferentzia

[4] Txantiloi:Erreferentzia

[5] Txantiloi:Erreferentzia

[6] Txantiloi:Erreferentzia

[7] Txantiloi:Erreferentzia

[8] Txantiloi:Erreferentzia

[:0-9] 9,0 ^9,1 Txantiloi:Erreferentzia

[10] Txantiloi:Erreferentzia

[11] Txantiloi:Erreferentzia

[12] Txantiloi:Erreferentzia

[13] Txantiloi:Erreferentzia

[14] Txantiloi:Erreferentzia

[15] Txantiloi:Erreferentzia

[16] Txantiloi:Erreferentzia

[17] Txantiloi:Erreferentzia

[18] Txantiloi:Erreferentzia

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

Bellen zenbaki

Edukiak

Pertsonen eta autoen arazoa

Historia